How To Use Kalman Filter In Matlab

Introduction to Kalman Filter Matlab

MATLAB provides a diversity of functionalities with real-life implications. This article covers a very important MATLAB functionality called the 'Kalman filter. We employ Kalman filter to estimate the state of a given system from the measured data. Once this is done, refinement of estimates is also washed. Let's starting time understand what the Kalman filter is.

What is Kalman Filter?

Kalman filter developed primarily by the Hungry-based Engineer, Mr. Rudolf Kalman, is an algorithm used to estimate state of a given system using measured data. The Kalman filter'southward algorithm is a 2-pace process. In the start step, the state of the system is predicted and in the 2nd step, estimates of the system land are refined using noisy measurements. Kalman filter has evolved a lot over fourth dimension and now its several variants are available. Kalman filters are used in applications that involve estimations, like figurer vision, navigation&guidance systems, signal processing, and econometrics.

Guidance, Navigation & Control

Kalman filters are used in guidance, navigation, and control systems. These filters synthesize position & velocity signals in sensor fusion. This is accomplished past fusing together GPS & IMU measurements (inertial measurement units). Kalman filters are ordinarily used in estimating the value of a point which cannot exist measured. For case, the temperature inside the aircraft engine or turbine, as temperature sensors would fail in such conditions. These filters are also used commonly along with LQR compensators (linear-quadratic-regulator) for LQG control(linear-quadratic-Gaussian).

At present that we have refreshed our agreement of Kalman filtering, let's see a detailed example to understand Kalman filter in MATLAB

Steps to Implement Kalman Filter in Matlab

Below are the steps user will demand to follow to implement Kalman filter in MATLAB. The MATLAB code is likewise provided forth with the steps:

i. Nosotros will define length of simulation:

simulen = thirty

2. Let us now define the organization

b = 1 c = 4

(we use b = 1 for constant systems; you lot can employ |b| < 1 for a system of i^st lodge)

three. Next, we volition declare the covariances of racket

Q=0.02; R=3;

4. Nosotros volition at present pre-allocate the memory for the arrays. Delight keep in mind that doing pre-allocation is not necessary, we only do information technology to speed-up the processing in MATLAB.

x=zeros(1,nlen); z=zeros(1,nlen);

5. Next, we will ascertain initial estimates for 'the state' and error ('priori error')

inpriori=zeros(1,nlen); inposteriori=zeros(i,nlen); residual=zeros(1,nlen); rapriori=ones(1,nlen); raposteriori=ones(1,nlen); g=zeros(1,nlen);

six. Next, we will compute the process noise and measurement noise

westward=randn(1, nlen); v1=randn(i,nlen);w=w1*sqrt(Q); v=v1*sqrt(R);

Here nosotros are taking percentage for a better comparing

seven. Let'southward now define initial condition on x and initial estimates for posteriori covariance and state

x_0= ii.0; inposteriori_0=one.5; raposteriori_0=ane;

eight. Next, we will compute the first guesses of all the values. This volition be done based on the initial estimates of state followed by posteriori covariance. Next steps will be computed in loopComputing land & output:

x(1)= b *x_0+w(1); z(1)= c *10(1)+v(1);

Our Predictor equations are:

inpriori(one)= b*inposteriori_0; residual(1)=z(1) – c *inpriori(1); rapriori(one)= b*b*raposteriori_0+Q;

Corrector equations volition be:

grand(1)= c *rapriori(1)/ (c * c *rapriori(1)+R); raposteriori(1)=rapriori(one)*(1 – h*g(i)); inposteriori(1)=inpriori(one)+grand(1)*residual(ane);

Computing rest values:

for p =2:nlen, ten(p) = b * ten(p -ane)+west(p); z(p) = c *x(p)+v(p); inpriori(p)= b *inposteriori(p-one); remainder(p)=z(p) – c *inpriori(p); rapriori(p)= b * b *raposteriori(p -1)+Q; thousand(p)= c *rapriori(p)/(c * c *rapriori(p)+R); raposteriori(p)=rapriori(p)*(1 – c *k(p)); inposteriori(p)=inpriori(p)+k(p)* residual(p); cease p =i:nlen;

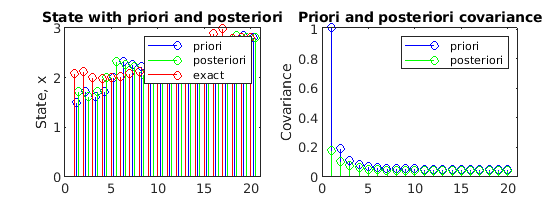
nine. Let'southward at present plot state & their estimates

subplot(221); h1=stalk(p +0.25,inpriori,'b'); hold on h2= stem(p +0.5,inposteriori,'one thousand'); h3=stalk(p,x,'r'); concur offlegend([h1(1) h2(1) h3(1)], 'priori', 'posteriori','exact'); title('State with priori and posteriori'); ylabel('State, x'); xlim=[0 length(p)+1]; prepare(gca,'XLim',xlim);

10. Let us too plot the covariance

subplot(222); h1= stem(p,rapriori,'b'); concur on; h2=stalk(p,raposteriori,'g'); hold off fable([h1(i) h2(1)], 'priori', 'posteriori'); title('Priori and posteriori covariance'); ylabel('Covariance'); set(gca,'XLim',xlim);

On implementing above lawmaking, below is how our output will look like in MATLAB:

Decision

Kalman filters are perfect for systems that are irresolute continuously. These filters have the reward of being lite on the memory as they don't require to proceed annihilation in history other than their previous state. Kalman filters are likewise very fast which make them peachy tool for embedded systems and existent-time problems.